Мы рождены... - часть 4

СЕЗАМ, ОТКРОЙСЯ !

Волшебное сказочное заклинание

Ой, мороз, мороз, не морозь меня…

Русская народная песня.

На практике изолированные термодинамические системы встречаются

крайне редко. Практически любой реальный объект представляет собой от-

крытую систему, имеющую какие-то границы (условные или физические).

Так, например, если рассматривать систему “жилой дом”, то ее границами бу-

дут стены здания, фундамент и крыша, если анализировать систему “террито-

рия области”, то за границы можно принять административные границы об-

ласти и т.д. В этом случае мы уже не можем считать, что подведенная извне

энергия “навсегда” останется в пределах границ, поскольку внешние условия

могут влиять на систему таким образом, что часть подведенной энергии поки-

нет пределы системы. Кроме того, в открытой системе возможно перемеще-

ние материальных объектов не только в пределах границ, но и за пределы сис-

темы (в ту или иную “сторону”), т.е. масса системы становится переменной

величиной.

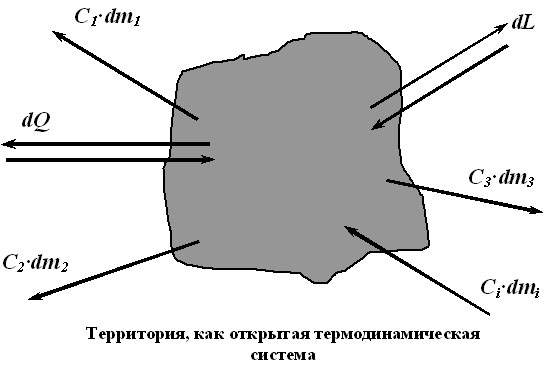
Для краткости в дальнейшем любой объект, в отношении которого бу-

дут проводиться рассуждения, назовем Территорией (территория комнаты,

микрорайона, области, страны, континента и т.д.). Теперь мы можем записать

уравнение Первого Закона термодинамики для Территории как для объекта с

переменной массой в виде:

dE = dQ + dL + dM , (3)

где dE — общее изменение энергии территории как системы, dQ — разность

между количеством энергии, поступившей в виде излучения Солнца, и коли-

чеством энергии излучения поверхности территории, dL изменение энергии,

обусловленное механическим движением природных материальных объек-

тов, dM — изменение энергии за счет изменения массы материальных объек-

тов, находящихся в пределах системы. При этом территорию можно считать

условно благополучной, если dE = 0 (по крайней мере — хуже не становится),

безусловно, угасающей, если dE < 0 (территория становится энергетически

беднее), и условно развивающейся при dE > 0 (энергия “прибывает”, накап-

ливается).

Знак “d”, стоящий перед обозначениями величин, составляющих баланс

энергии, — это знак дифференциала — основной части приращения (изменения)

функции (математически выраженной зависимости одной или нескольких ве-

личин от другой или других величин).

Физический смысл уравнения (3) можно пояснить на простом примере.

Пусть на произвольно выбранной Территории одновременно в некоторый

(i-тый) момент времени поступило dm1 некоторого топлива и вывезено dm2

некоторого продукта. В этом случае величина dMi , характеризующая изме-

нение энергии, зависящей от массы территории, определится так:

dM_i = C₁ × dm₁ ×h — C₂ × dm₂ + C₃ × dm₃

где С1 — теплотворная способность привезенного топлива, h — обобщенный

КПД превращения массы dm1 топлива в необходимые виды энергии, С2 —

удельные энергетические затраты, понесенные при изготовлении вышена-

званного продукта, dm3.- отходы, полученные при сжигании топлива (напри-

мер, зола — при сжигании угля), С3 — удельные энергетические затраты, необходимые для добычи строительного материала, который может быть заменен золой.

Положим также, что в данный момент времени за счет механического

движения водных и воздушных масс получена энергия (например, в виде

электрической энергии), часть которой (dL1) израсходована на нужды терри-

тории, а другая часть (dL2) передана на другие территории. В этом случае —

dL_i = dL₁ — dL₂ .

Определение размеров dQi пояснений не требует.

Теперь от абстрактной (мысленной) модели перейдем к конкретной

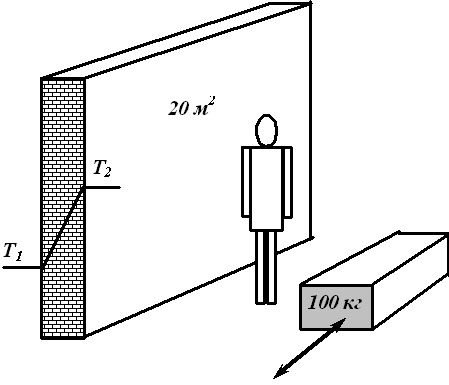
и рассмотрим следующий пример. В качестве исследуемой Территории возь-

мем небольшое производственное помещение с наружной стеной всего

в 20 квадратных метров (м² ), для простоты счета — без окна. Толщина стены —

0,6 м, материал — кирпич с коэффициентом теплопроводности

l = 0,95 вт/м·градус. Теплоту проводит только эта лицевая стенка, так как

помещение со всех сторон примыкает к другим аналогичным комнатам.

На Территории находится человек. Он дышит (17 кг свежего воздуха

в сутки), умывается и пьет воду (10 кг свежей воды в сутки) а также обраба-

тывает стальные детали, общим весом в 100 кг, которые попадают к нему

с улицы. Температура на улице — Т1, в помещении Т2 = +20⁰ С.

Рассмотрим сравнение двух вариантов существования Территории –

в Сибири и в южной полосе США в зимний период, когда в Сибири средняя

температура улицы около -10⁰ С (мягкая зима), а в США +20⁰ С. Предполо-

жим, что в обоих случаях ресурсов вполне достаточно для обеспечения благо-

получия и dE = 0.

Тогда уравнение Первого Закона термодинамики будет иметь следую-

щий вид:

dQ + dL + S × dМ = 0

Проанализируем каждое слагаемое в отдельности.

Изменение энергии за счет солнечного излучения dQ — в данном случае

рассматривать не имеет смысла, т.к. мы сами на основе объективных наблю-

дений задались внешней и внутренней температурами, и без существенной

погрешности можем предположить, что температура стенок соответствует

температуре воздуха — наружная стенка имеет в Сибири температуру -10⁰ С, в

США +20⁰ С, температура внутренних стенок в обоих случаях равна +20⁰ С.

Величина dL в обоих случаях одинакова (одинаковые детали и одинако-

вая производительность труда) и ее можно исключить из рассмотрения.

Сумма (заглавная греческая буква S — сигма, означает в математике

сумму) изменения энергии за счет изменения массы определится следующим

образом.

1. Приток свежего воздуха. В Сибири нужно согреть за сутки 17 кг воз-

духа от температуры -10⁰ С до температуры +20⁰ С, т.е. на 30⁰ . Для этого нуж-

но удельную теплоемкость СР воздуха умножить на массу dm = 17 кг и на раз-

ность температур 30⁰ . Получим: dM1 = 1005*17*30 = 512550 Дж/сутки.

В США для согрева воздуха тратить энергию не нужно.

2. Подогрев воды. Положим, что вода в Сибири зимой из под крана идет

с температурой +8⁰ С, тогда, будучи вылитая в помещении с температурой

+20⁰ С, она нагреется на 12⁰ С, отобрав энергию, которую аналогично п.1

можно рассчитать следующим образом: dM2 = 4200*10*12 = 504000

Дж/сутки.

В США для согрева воды тратить энергию не нужно.

3. Подогрев объекта труда. Объект труда подается с улицы, например,

с холодного склада, или привозится автотранспортом и имеет температуру

улицы. В процессе обработки он приобретает температуру помещения, т.е. со-

гревается всего на 30⁰С. Аналогично п. 1 и 2 произведем расчет

dM3 = 440*100*30 = 1320000 Дж/сутки.

В США подогревать объект труда не нужно.

4. Компенсация тепловых потерь через стену. Для этого необходимо

воспользоваться уравнением (2), в котором величина (Т1 — Т2) = 30⁰ С, l =

0,6 м, F = 20м² , l = 0,95 Вт/м*градус, t = 24 часа*60 минут*60 секунд =

86400 с. Теперь можно сделать расчет:

dM4 = 0,95× —- × 20×86400= 82080000 Дж сутки/

0,6

В США компенсировать тепловые потери через стенку не нужно.

Таким образом, величина S dM = 512550 + 504000 + 1320000 + 82080000 =

84416550 Дж/сутки = 84416,55 кДж/сутки.

Если мы будем отапливать помещение углем с теплотворной способно-

стью СВ = 18000 кДж/кг, и КПД отопительной системы h (КПД котла, сопро-

тивление подводящих трубопроводов и потери теплоты в них в тепловой се-

ти) равен 0,65, (что примерно соответствует существующей реальности ), то

получим, что для компенсации всех тепловых затрат нам нужно ежесуточно

сжигать:

SdM 84416 55,

m = —— = ——— = 7 215, кг угля в сутки

CВ ×h 18000×0,65

или примерно 216,5 кг угля в месяц. Если бы мы сделали расчет для железо-

бетонной стены (что, зачастую и имеет место для производственных помеще-

ний) то получили бы результат, примерно в два раза больший. Если бы учли

наличие окон, то результат был бы еще примерно в 1,5 раза больший.

При этих же условиях в США не нужно совсем тратить топлива на под-

держание нормальных условий жизнедеятельности.

Следует обратить внимание на превалирующее влияние низкой наруж-

ной температуры на необходимость вводить в термодинамическую систему

массу вещества, чтобы сохранить ее благополучие и выполнить условие Пер-

вого Закона термодинамики.

Как видим, с расчетами для одного небольшого производственного по-

мещения мы разделались довольно быстро, и рассуждения сильно не огрубля-

ли (то есть не принимали допущений, которые кардинально повлияли

бы на величину результата). Чего мы еще не учли? Ну, например, разницу

в продолжительности светового дня, который у нас зимой значительно коро-

че, чем на юге США, из-за чего за сутки в Сибири в зимнее время при мощно-

сти лампочки в 100 Вт мы потратим — 16 часов ´ 60 минут ´ 60 секунд ´ 0,1

кВт = = 5760 кДж энергии, или 6,8 % от прежнего результата, а в США при

10-ти часовом освещении — 4,25 %. Не учитывали мы и разницу в затратах

энергии на питание, одежду и т.д. Вероятно, что все вместе огрехи не превы-

сят 50 %, что уже можно считать удовлетворительным.

Но как быть, если анализируемый объект намного сложнее? Ну, напри-

мер, мы попытаемся “рассчитать” энергетический баланс целой области?

Сколько материальных объектов пересекает ее границы в ту, и в другую сторо

ну в достаточно большой контролируемый промежуток времени? Сколько

джоулей “стоит” каждый объект и можно ли их все “засечь”? Во что реально

выльется попытка такого расчета? Сколько уравнений вида (3) придется со-

ставить, и возможно ли будет решить систему таких уравнений?

Нет, уважаемый Читатель, абсолютно точно, как задачу из учебника,

в конце которого всегда есть готовый ответ, эту проблему решить невозмож-

но. Тогда стоит ли ей заниматься? А если она слишком сложна, то есть ли

другие не менее объективные и строго научные методы выяснения основ жиз-

недеятельности (и даже живучести) тепловой цивилизации?

Затронутая проблема является чисто математической, а если точнее –

она относится к методам решения систем нелинейных алгебраических урав-

нений, которые достаточно хорошо разработаны и широко используются

при решении технических и экономических задач.

Весь вопрос состоит в том, с какой степенью приближения решать та-

кую задачу, какие факторы считать точнее, и чем можно пренебречь. Так, на-

пример, существовали полученные расчетным путем нормативы, в которых по

ежедневному весу снимаемой в конкретном производстве металлической

стружки определяли размер капитальных затрат на создание целого машино-

строительного предприятия!

В рассматриваемой нами задаче есть еще одна проблема, без решения

которой никак не обойтись. Если помните, в Первом Законе термодинамики

для изолированной системы, — уравнение (1), — мы использовали такое понятие

как “внутренняя энергия” (обозначение — dU — изменение внутренней энер-

гии). Куда она девалась теперь, когда мы “отрыли” систему? Испарилась,

что ли? В принципе, часть этой энергии или вся она может действительно,

в полном смысле слова и испариться, если эта энергия поступила на террито-

рию в виде жидкости (например — речной поток). Но речь, конечно, идет

не только о воде.

Тогда давайте рассуждать так. Мы говорили о том, что если “приход”

и “расход” энергии равны между собой (dE = 0), то мы имеем дело с благопо-

лучной системой (благополучной Территорией). Однако, каков уровень этого

благополучия?

Представим себе такую ситуацию. Двое людей — один бедный и боль-

ной, живет в “хрущевке”, другой богатый и здоровый, живет в коттедже. У

обоих в рассматриваемый период времени одинаковая зарплата, которую

они оба полностью тратят “на жизнь”. Кто из них реально живет лучше? (Во-

прос, как говорят, риторический, т.е. не требующий ответа). Тогда возникает

другой вопрос, как возникла такая ситуация?

Если не рассматривать социальную сторону заданного вопроса, то со-

вершенно ясно, что были времена, когда живущий сегодня в коттедже полу-

чал в свое распоряжение гораздо большее количество денежных средств, ко-

торые он обменивал на строительный материал, рабочую силу, услуги врачей

и т.д. Сегодня этих средств уже нет, они потрачены, исчезли. Осталось только

хорошее здоровье и прекрасное жилье. Может быть, это и есть та самая

“внутренняя энергия”, овеществленная в благосостоянии?

Давайте снова вернемся к цилиндру с поршнем. Там мы ввели в систему

некоторое количество тепловой энергии, благодаря чему повысили внутрен-

нюю энергию и совершили механическую работу. Если мы захотим, то можем

“вернуть назад” затраченную теплоту (не всю, конечно, но в идеале, большую

часть), введя в цилиндр теплообменник и с помощью теплоносителя (напри-

мер, с помощью воды, подобно радиатору в автомобиле) отведем (“откачаем”)

теплоту от газа и потратим на что-нибудь другое, более нужное. Поршень

при этом должен вернуться в положение, близкое к исходному.

Внутренняя энергия в этом случае сыграла роль потенциальной, закон-

сервированной энергии — подержали ее в цилиндре (как в термосе), а потом

использовали по назначению.

Можно ли таким же образом рассуждать по отношению, например,

к коттеджу?

В какой-то степени — да. В нем тоже “законсервирована” потраченная на

его создание энергия. Вот только “изъять” и потратить ее на что-нибудь дру-

гое уже вряд ли удастся. Разве что разобрать коттедж по кирпичику, и добы-

тый таким образом стройматериал направить на другое строительство? Но,

строго говоря, такой кирпич будет наверняка стоить (в тепловых единицах)

существенно дороже нового.

Итак, хотя вопрос с внутренней энергией пока у нас “повис”, мы выяс-

нили, что часть поступающей на территорию энергии (в том числе и в матери-

альном виде) практически навсегда исчезает из “энергетического оборота”.

По крайней мере, это полностью соответствует для недвижимости, которая

потому так и называется, что фактически не может быть “передвинута” за

пределы Территории. Сюда же можно отнести и такие объекты как автомо-

бильные и железные дороги, мосты, тоннели, стадионы и библиотеки, разра-

ботанные месторождения т.д.

Таким образом, за все время существования Территории она может на-

капливать некоторые ценности (в общем понимании этого слова) за счет не-

эквивалентного обмена с другими Территориями (больше энергии “привозит”

и меньше “вывозит”) и за счет получения энергии внутри системы, которая

либо накапливается подобно внутренней энергии и может быть в любой мо-

мент реализована на нужды Территории, либо расходуется. Последнее может

осуществляться и для компенсации неэквивалентного обмена (если Террито-

рия больше “вывозит” и меньше “привозит”). Главное, чтобы, в конце концов,

выполнялось условие dE > 0.

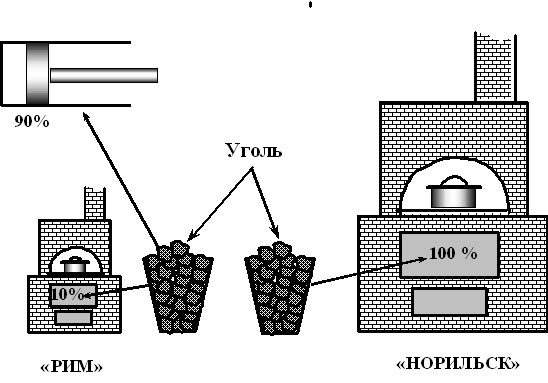
Куда и как девать “излишки” энергии? Рассмотрим такой примитивный

случай. На двух далеко отстоящих широтах (например — на широте Норильска

и на широте Рима) в некоторые незапамятные времена два человека, обла-

дающие одинаковыми физическими возможностями, добыли “вручную” за

день по ведру угля. Северянин все ведро вынужден сжечь в печке, чтобы со-

греть жилище и приготовить пищу. Римлянин на эти цели потратил 10 % угля,

а остальные 90 % пустил в дело — например, сжег в котле паровой машины,

чтобы получить механическую работу, или смешал с железной рудой и вы-

плавил сталь.

Итак, добыто одинаковое количество энергоресурсов, но потрачены

они по-разному и с разным результатом. Северянин только-только обеспечил

минимальные человеческие потребности и остался на прежнем уровне разви-

тия, римлянин продвинулся вперед на пути “технологического прогресса”.

Цифры 10 % и 90 % взяты чисто условно, вполне вероятно, что в Но-

рильске нужно в день на человека сжигать далеко не по одному ведру угля,

а в Риме его на отопление и вовсе жечь не надо. Главное, что хотелось бы

продемонстрировать этим примером — разное географическое и климатическое

положение Территории требует количественно и качественно разного потреб-

ления энергии для достижения одних и тех же целей. Тогда можно попытать-

ся представить себе некий энергетический потенциал Территории ЕК,

который определяется как количеством потраченной энергии, так и эффек-

тивностью ее использования:

^i=k

Е_k= ( E_i×a_i×b_i×c_{_i}). (4 )

i=1

В уравнении (4) Еi — количество энергии, полученной Территорией на

i—том отрезке времени стабильного технологического развития, a — коэффи-

циент, учитывающий уровень ее технологического развития, b — коэффици-

ент, показывающий, какая доля энергии в i—том периоде тратилась на анали-

зируемой Территории для осуществления целей, соответствующих k-тому

(сегодняшнему) отрезку времени, с — коэффициент, учитывающий долю

энергии, минимальный объем которой необходим для поддержания жизне-

деятельности. Вполне естественно каждый раз принимать a = 1(т.е. сего-

дняшний, k—тый уровень развития принимаем за единицу — эталон). Так, на-

пример, в начале 20-го века (i < k; a < 1) на одной и той же террито-

рии 1 джоуль энергии можно было превратить в гораздо меньшее количество

благ, чем сегодня ( i = k; a = 1) .

С другой стороны, если, например, считать, что для поддержания вели-

кодержавного курса СССР в послевоенный период на вооружение тратилось

до 70 % ресурсов страны вместо, положим, действительно необходимых

(с сегодняшней, «k-той» точки зрения) 35 %, то при вычислении величины Еk

придется принять bi < 1 (в данном случае i-тый период — период гонки воору-

жений). Нужно отметить, что при сравнении территорий с явно отличными

друг от друга Еk получаются весьма впечатляющие результаты. Так, напри-

мер, если в 1863 году в Англии была пущена первая ветка метрополитена,

то в России — только отменено крепостное право.

Таким образом, мы имеем в своем распоряжении два основных инстру-

мента:

1. Первый Закон термодинамики для открытой Территории.

2. Положение об Энергетическом потенциале.

Эти инструменты позволяют производить количественное измерение

нашего благосостояния, объективно сравнивать различные Территории, коли-

чественно оценивать материальные объекты в тепловых (энергетических)

единицах.

Следует отметить, что если уравнение (3) Первого Закона термодинами-

ки является “абсолютно” точным (в рамках сегодняшнего представления о

мироздании), то уравнение (4), описывающее Энергетический потенциал, та-

ковым назвать нельзя. В нем присутствуют субъективные оценки уровня тех-

нологического развития (величины коэффициентов). В связи с этим абсолют-

ная величина Еk анализируемой Территории будет колебаться в зависимости

от назначенных нами величин критериев. Но, тем не менее, он дает возмож-

ность сравнивать разные Территории по уровню технологического развития

и этим сильно напоминает так и не определенную нами внутреннюю энергию.