НОВОЕ ПРЕДСТАВЛЕНИЕ СИММЕТРИИ МЕЖДУ ЗАПОЛНЕНИЕМ ЭЛЕКТРОННЫХ ОБОЛОЧЕК ХИМИЧЕСКИХ ЭЛЕМЕНТОВ И СПЕКТРОМ АТОМА ВОДОРОДА

Автор: профессор Юрий Магаршак.

В 2006 году в работе [1] была показана симметрия между заполнением подоболочек элементов периодической системы как функции порядкового номера химического элемента и спектром атома водорода с точностью до поворота на угол π/4 на плоскости главного и орбитального квантовых чисел (сокращенно называемая H—subshells симметрией, или при сокращении до трех букв HSS симметрией). Этот воспроизведенный в ряде работ рисунок (в цитируемой работе имевший номер 4) приводится на рисунке 1 настоящей работы.

Рисунок 1

Несмотря на усилия математиков и физиков теоретиков, вывести указанную симметрию из уравнения Шредингера не удается. Трудность состоит в повороте между симметриями на π/4, поскольку ни сферические, ни какие-либо другие специальные функции решений с поворотом на этот угол ни в уравнении Шредингера, ни подобных уравнению Шредингера уравнениях, не дают.

Обнаруженный феномен в принципе может быть объяснен двумя способами.

1. HSS -симметрия является не законом природы, а эмпирическим соотношением[1], которое математически получается приближенными компьютерными вычислениями, а потому никаких физических обоснований не требует.
2. HSS—симметрия генерируется квантовополевыми процессами взаимодействия электронной оболочки с ядром.

Первый ответ возможен и традиционен, хотя его вероятность крайне мала. На рисунке 2 приведен порядок заполнения электронных оболочек первых ста четырех элементов периодической системы [5] как функции порядкового номера элемента. Элементы по горизонтали упорядочены как это следует из уравнения Шредингера: оболочки ->подоболочки.

[1]Вспомним, что правило Хунда 1926 года [2], объявлено эмпирическим соотношением а не Законом Природы по той же самой причине: потому, что из уравнения Шредингера вывести его не удалось. Так же, как не удаётся аналитически вывести из уравнения Шредингера правило Маделунга [3], в России и некоторых других странах называемое правилом Клечковского [4] несмотря на то, что работа Клечковского была опубликована на четверть века позднее.

Рисунок 2

Как видим, регулярность заполнения электронных оболочек атомов (химических элементов) при традиционном упорядочении (оболочки =>подоболочки) нарушена. Однако если упорядочение по горизонтали производить так, как это сделано на рисунке 3, заполнение электронных оболочек вдоль диагонали рисунка становится (за редкими исключениями) регулярным.

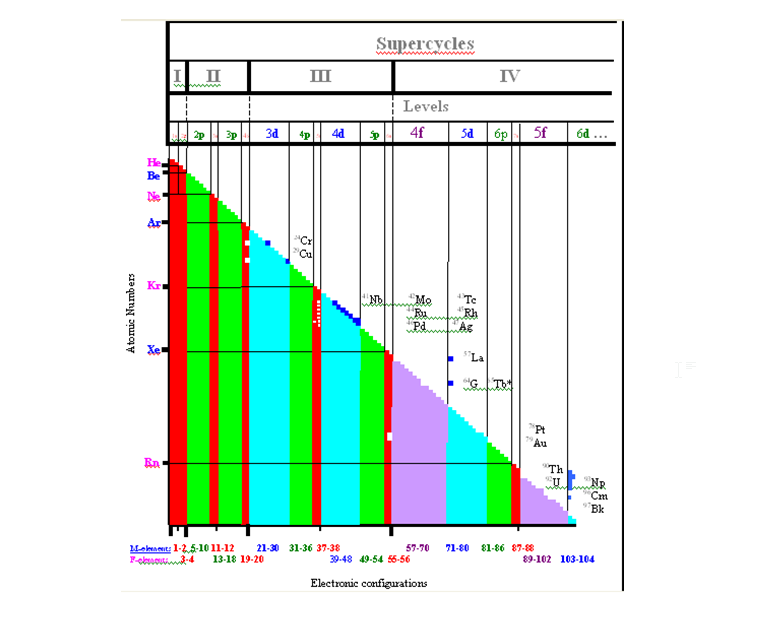
Рисунок 3

Регулярность заполнения электронных оболочек (рисунок 3) возникает в том случае, если упорядочение по горизонтали производится не так, как это делается со времен Менделева, а иначе. А именно: по суперциклам, циклам и уровням (supercycles, cycles and levels).При этом число элементов в циклах равно 2,2; 8,8;18,18; 32,32… , то есть 2k²  где к=1,2,3,4 . Число элементов в суперциклах равно (2k)²  где k=1,2,3,4.

Все открытые в настоящее время химические элементы могут быть разделены на восемь циклов и четыре суперцикла. Число элементов в циклах (и уровнях) 2,2; 8,8; 18,18; 32,32. Число элементов в суперциклах 4,16, 36, 84, то есть k² где  k=1,2,3,4. При этом с увеличением атомного номера происходит генерация элементов каждого уровня сначала M-цикла, затем F-цикла этого же суперцикла, на рисунке 3 слева направо.

Как было впервые показано в работе [6], упорядочение по циклам и суперциклам (в котором каждый цикл щелочными и щелочноземельными металлами не начинается, как в Периодическом Законе принято с Менделеева и по сей день, а заканчивается) приводит к обнаружению в периодической системе третьего [7] (а также четвертого [1,6]) измерений, и к пирамидам атомов (в химии называемых элементами [1]).На рисунке 4 изображена Пирамида Атомов и Химических Элементов, в том виде, в каком она впервые была представлена на рисунке 8b работы [1].

Рисунок 4. Пирамида атомов и химических элементов с симметриями по вертикалям, горизонталям и диагоналям.

Упорядочение по циклам и суперциклам рисунка 3 приводит к HSS—симметрии. Отклонения от упорядоченности (заполнения подоболочек и оболочек по диагонали рисунка 3), как следует из рисунка 3, крайне редки.

Возможно ли, что столь высокая упорядоченность возникает не как результат физического процесса (закон природы), а как артефакт решения уравнения Шредингера, то есть как чисто эмпирический результат, который аналитически получить невозможно? Ответ, который не следует исключать, но (как видно из рисунка 3) представляющийся маловероятным. Являющийся, несмотря на это, в настоящее время традиционным. Отчасти и потому, что вопрос о HSS –симметрии как самостоятельная проблема не ставился.

Независимо от того, является ли HSS-симметрия побочным результатом решения уравнения Шредингера,или она генерируется не только уравнением Шредингера для заполнения электронных оболочек атомов, но и другими физическими процессами, нахождение и анализ представлений HSS – симметрии представляется необходимым.

На рисунке 5 изображено отличное от рисунка 2 представление HSS – симметрии. Вывод которого проводится в работе [9], а также в статьях, которые появятся в ближайшее время.

Рисунок 5

Поворот вертикальной оси рисунка 5 на 45 градусов по часовой стрелке генерирует представление периодических свойств атомов, представленное на рисунке 6.

Рисунок 6

На этом рисунке последовательность заполнения электронных оболочек всех атомов как функции заряда ядра происходит сверху вниз, в то время, как заполнение электронных подоболочек электронной оболочки за номером k происходит диагонально снизу вверх и слева направо.

На рисунке 7 изображен только порядок заполнения циклов рисунка 6.  Напомним, что координаты на этом рисунке (n+l, n-l) повернуты относительно порядка заполнения оболочек и подоболочек в атоме водорода на π/4.

Рисунок 7

Если объединить циклы, имеющие одинаковую структуру (состоящие из одинакового числа подоболочек) в суперциклы, получаем рисунок 8.

Рисунок 8

Или, если ограничиться изображением порядка заполнения циклов в суперциклах, получаем рисунок 9:

Рисунок 9

После чего тождественность структуры заполнения суперциклов с структурой спектра атома водорода очевидна.

Рисунки 5-9 показывают, что HSS—симметрия может определяться уравнением Шредингера или подобным уравнению Шредингера с дополнительным квантовым числом (получившим название Phys—Chem quantum number), не являющимся электронным спином. При этом:

1. HSS—симметрия возникает не в координатах главного n и орбитального lквантовых чисел, а в координатах (n+l,n—l) после их поворота на угол π/4.
2. Заполнение циклов происходит начиная не с минимального орбитального квантового числа l, а максимального l, и не с увеличением l, а с его уменьшением.
3. При заполнении электронных оболочек атомов согласно уравнению Шредингера в валентных частях периодов периодической системы (первые десять этажей пирамиды элементов (рисунок 4) или прямоугольной части Периодической Системы в её традиционных изображениях, в которых химические элементы подразделяются на периоды и группы) орбитали заполняются электронами с противоположными спинами. В противоположность этому суперциклы и циклы периодической системы заполняются так, что сначала заполняются орбитали одного цикла, потом другого. Заполнение каждого следующего цикла начинается после завершения заполнения предыдущего – в отличие от того, как это происходит с электронными оболочками атомов с учетом электронного спина в качестве четвертого квантового числа.

Таким образом, HSS-симметрия в принципе может быть выведена из уравнения Шредингера или уравнения, подобного Шредингеровскому, в то же время существенно отличаясь от его решения для атома водорода и квантовомеханического объяснения периодического закона с четырьмя квантовыми числами (главным, орбитальным, магнитным и спином). Наличие нетривиальных симметрий в периодической системе (смотри, например, выдержавшую несколько изданий монографию А.Сисакяна и Г. Погосяна [9]), и даже в решениях уравнения Шредингера для атома водорода, впервые продемонстрированных в ставших классическими работах Фока 1935 года (V,Fock, Hydrogen atom and non Euclidean geometry [10,11]) не вызывает сомнений.  В том случае, если HSS-симметрия генерируется не приближенными вычислениями, а физическим процессом, дополняющим традиционную модели атома, природа HSS-симметрии представляется интригующей и важной проблемой. Работа в этом направлении ведется [12-15].

ЛИТЕРАТУРА

• Magarshak, «Four-Dimensional Pyramidal Structure of the Periodic Properties of Atoms and Chemical Elements«, Scientific Israel — Technological Advantages vol. 7, No.1,2 , pp. 134-150 (2006)
• Hund, ZeitschriftfürPhysik, 36(1926), 657
• Madelung Die mathematischenHilfsmittel des Physikers, 3rd ed. Springer, Berlin, 3^rded., 359, (1936).
• Klechkowski, V. M., Zh. Exsperim. iTeor. Fiz., 23(1952), 115.
• Bogomolov, Y.Magarshak, On commuting operators related to asymptotic symmetries in the atomic theory; Scientific Israel-Technological Advantages, vol 8, issues 1-2,  pp. 161-165 (2006)
• Magarshak, The third and the fourth dimensions of the chemical elements periodicity, Biophysics, vol. 50 number 4 (2005)
• Magarshak Y., Malinsky J., A three-dimensional periodic table, Nature, vol.360, 114-115 (1992).
• Юрий Магаршак МНОГОМЕРНЫЕ СИММЕТРИИ В ПЕРИОДИЧЕСКОМ ЗАКОНЕ. Монография. Media Publishing House, 2018.
• Мардоян Л.Г., Погосян Г.С., Сисакян А.Н., Тер-Антонян В.М. «Квантовые системы со скрытой симметрией. Межбазисные разложения Москва Физматлит 1985 год
• Fock, ZürTheorie des Wasserstoffatoms;Z. Phys. 98, 145-154 (1935)
• V,Fock, Hydrogen atom and non Euclidean geometry; Proc. of the Academy of Sc. of the USSR, , v.2, 169-179, (1935).
• Magarshak Ellectron-Nucleons Resonance Atom Model of valence bonds. J Nuclear Physics, v. 71 #5, pp 1-9 (2008)
• Magarshak, “Superresonant Atom Model as an element of the united theory of matter”.  Scientific Israel – Technological Advantages (SITA) vol. 10 pp.145-150 (2008)
• Bogomolov Yu.Magarshak Chemical Elements as the States of I-particle Scientific Israel — Technological Advantages Journal (SITA) volume 9, issue 1 (2007)
• A. Gribov, Y.B. Magarshak, To the Problem of Formulation of Basic Principles in the Theory of the Molecular Structure and Dynamics Concepts of Physics vol.V Nr.2 p 191 (2008)

Иллюстрация: ЕДИНИЦЫ ИЗМЕРЕНИЯ
Симметрия