«Вначале существовал лишь Хаос».
Легенды и мифы древней Греции.
«В природе нет случайности. Вещь может казаться случайной только из-за неполноты нашего знания».
Барух Спиноза.
Я долго думал, как лучше назвать то, о чём я собираюсь написать. А собираюсь я показать в картинках, что и в хаосе можно при желании найти порядок, и из хаоса может получиться порядок, да такой, что и не скажешь, что это получилось из хаоса.
Все картинки, которые будут показаны, получены на компьютере с помощью программ, называемых датчиками случайных чисел. Эти программы широко используются в научных экспериментах по моделированию разных явлений методом «Монте-Карло», иными словами методом тыка. Для того, чтобы метод тыка дал хорошие результаты, нужно уметь по возможности равномерно перебирать возможные варианты. Для этого и нужны хорошие «датчики случайных чисел». А вот если датчик не очень хорош, он дает преимущественно одни варианты, и не дает другие, сколько его ни гоняй.
Эти числа называются случайными чисто условно для непрофессионалов. На профессиональном языке их называют «псевдослучайными», имея в виду, что они только кажутся «случайными». На самом деле эти числа получаются от одного и того же числа, называемого «зародыш», одно число за другим. Для каждого следующего числа «зародышем», является предыдущее. Делается очень просто. Предыдущее число умножается на некоторое постоянное число, затем к результату прибавляется другое постоянное число, и следующее «псевдослучайное» число получается как остаток от деления полученной суммы на некоторое третье число. Последняя операция называется «вычислением по модулю». Собака зарыта в этой последней операции. После нее уже невозможно узнать, какое число было в начале.
Построить «хороший» датчик случайных чисел – большое искусство. Для этого нужно очень тщательно выбрать упомянутые три константы. Недаром отец современных компьютеров замечательный математик Джон Фон Нейман писал: «Если кто-нибудь думает, что с помощью арифметических действий можно создать случайные числа, то он, конечно, сумасшедший».
Вот как выглядит последовательность более или менее «хороших» псевдослучайных чисел, созданная одной из самых распространенных стандарьных программ-генераторов псевдослучайных чисел, если эти числа представить как «пиксели», то есть отдельные точки, картинки:
Она выглядит в общем-то хаотически, хотя иной читатель, всмотревшись, может быть и увидит какие-нибудь осмысленные узоры, как иногда ночью в темном лесу нам порой может померещиться всякая чертовщина.
А вот, что получится, если в этой программе немного изменить её числовые параметры.
Не правда ли, похоже на капли дождя в дождливый день? Хаотично, но явно ощущается некоторый «порядок». Или вот еще примеры:
Она вроде бы и хаотична, но монеты явно распределились неравномерно по поверхности стола, хотя казалось бы, монеты должны были бы быть распределены равномерно по площади, так как датчик обещает это обещает. На картинке явно видно, что они образуют сгущения, или кластеры. В этом «хаосе» угадывается некий порядок. Может быть с датчиком что-то не в порядке?
Но это все примеры того, что дает непосредственно датчик «случайных» чисел, если изменять три его числовые параметра. А какое разнообразие можно получить, манипулируя всячески с этими случайными числами!
Начнем с того, что зелёный фон предыдущей картинки (зеленый «стол», на который падают монеты) получен из случайных чисел показанных на самом первом рисунке путем их модификации, направленной на имитацию текстуры ткани. И эти кружева тоже получены из той же начальной хаотичной картины.
Напомним, что все эти картинки получены из исходных хаотичных картинок, пример которых был показан в самом начале, а сами эти исходные картинки получаются в пиксель за пикселем, строка за строкой из одного числа, «зародыша», в процессе эволюции через некоторое число шагов (итераций). Показанные выше картинки – ветви на дереве такой эволюции. На них эволюция была остановлена. Это как бы «ископаемые остатки».
А что если сделать так, чтобы на каждом шаге итерации каждый пиксель изменялся в зависимости не только от «предыдущего» пикселя в процессе сканирования, а от своего окружения сверху, снизу и с боков по определенным правилам, содержащим необратимые операции?
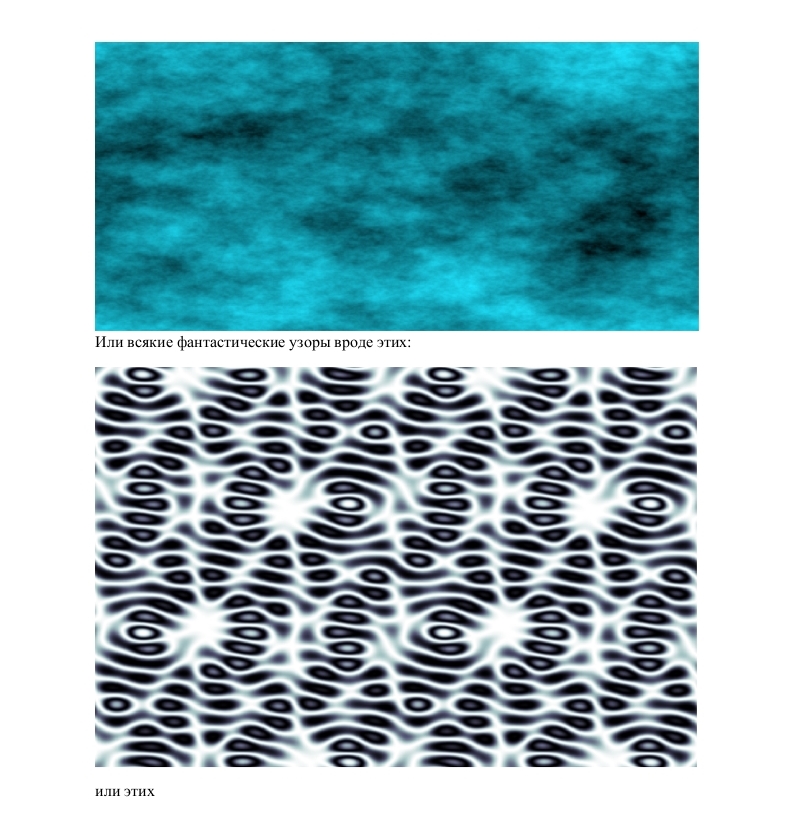
Вот тут начинаются ещё более удивительные явления. При определенных правилах она порождает фантастический мир узоров. Одни из них, единожды возникнув, остаются потом неизменными. Другие, оставаясь стабильными, демонстрируют временнЫе циклы: если на них смотреть, иные из них напоминают мерцающие созвездия, иные – как маятники, как например, узор известный под названием «светофор»: горизонтальная черта переходит на следующем шаге в вертикальную, а та потом обратно в горизонтальную, и так до бесконечности. Третьи, так называемые «планеры»», вообще движутся по полю с каждым шагом эволюции, пока не наткнутся на один из стабильных или периодических узоров. Тогда происходит взрыв, узоры разрушаюся, и из нового хаоса потом постепенно рождаются новые стабильные, периодические или подвижные узоры. Вот один из примеров, пролученных на модели британского математика Дж. Конвэя, которая называется «Игра жизнь» (Game of Life)
Жаль, что нет возможности показать этот дивный мир в движении. Это все можно запустить и в трех измерениях, то есть в объеме. Вот только визуализировать и наблюдать это непросто.
Закономерности этого эволюционного поведения очень поучительны и во многом не изучены. А они важны для понимания многих естественных явлений, таких, например, как рост и взаимодействие клеток в живых организмах или формирование стай птиц. Это предмет науки нелинейной динамики и детерминистического хаоса. Детерминистического, потому что все начинается с одного числа и происходит по фиксированным и известным законам. Но вот необратимость в процессе эволюции и создает этот невообразимо богатый мир.
Так что на вопрос, что может получиться из хаоса, ответ: все что угодно! Лишь бы хаос был хороший!