Этот расчудесный мир- хаос out гармония in
Д-р Давид Гафт
Сотворение Адама Микеланджело, около 1511 года.
Вместо предисловия
Хаос или »эффект бабочки»
Не было гвоздя — Подкова пропала. Не было подковы — Лошадь захромала. Лошадь захромала — Командир убит. Конница разбита — Армия бежит. Враг вступает в город, Пленных не щадя, Оттого, что в кузнице. Не было гвоздя.
Самуил Маршак
Дорогие читатели, наверное, многие из вас знают, что такое »эффект бабочки». Так вот у меня этой »бабочкой» являлись 10 копеек!!! Будучи школьником в семидесятые годы прошлого столетия, на Украине за 10 копеек можно было купить стакан подсолнечных семечек. Семечки подсолнуха – национальный украинский продукт, украинский попкорн и прочие лакомства. Не всегда в кармане находилась такая »большая сумма денег». Благо, что поля моего региона были усажены подсолнечником, и можно было поживиться семечками, прямо срывая цветки подсолнуха. Ещё тогда меня удивляло, что семечки строго упорядочены в два ряда спиралей, один против другого. Конечно, причину такой закономерности я тогда понять не мог. Прошло много лет, и, изучая математику, я вспомнил мои детские впечатления и в какой — то степени получил на это ответ. Возможно, поэтому я пытался в своих статьях реализовывать концепцию математических моделей. Математические модели, по моему мнению, дают количественный анализ происходящего, а не только субъективное качественное описание. «На кончике пера» открываются новые математические модели, которые предполагают возможность предсказывать поведение реальных объектов или тех или иных процессов. Математика — это язык, придуманный людьми именно для описания реальности, без которого ни одна наука не может существовать.
Одной из целей данной статьи является заинтересовать или даже стимулировать читателей видеть наш мир другими глазами. Глазами чисел и закономерностей.
Бог – непостижимый и могущественный математик
Математика – королева и служанка наук
Эрик Темпл Белл
Математика – это больше чем наука, это язык науки
Нильс Бор
Конечно же, когда Бог занимался творением нашего мира1 за семь дней (на седьмой день Творец отдыхал), он досконально »знал» математику, то есть создавал в соответствии с математическими правилами, чтобы человечество шаг за шагом могло частично распознать умысел Его творения!!! Другими словами, Творец является математиком недостижимо высокого ранга. Известно высказывание Вильгельма Лейбница2 математика, логика, философа и физика: »Геометрия есть сам Бог,… и служит его прообразом при сотворении мира». Более 2300 лет назад греческий математик и философ Пифагор3 считал, что он открыл принцип, согласно которому устроен мир (конечно, звучит очень самонадеянно). Его ученики и последователи писали, что если Бог создавал мир, то Пифагору удалось рассуждать подобно Богу, и эти рассуждения оказались математическими. Ещё один тезис выдвинула Пифагорейская школа: »Числа правят миром». Платон4, сделал еще один гениальный вывод – мир един, ибо он имеет единое начало – источник всего сущего, великую изначальную силу, рождающую Вселенную. В 1933 году Эйнштейн5,6 писал: “Весь предшествующий опыт убеждает нас в том, что природа представляет собой реализацию простейших математически мыслимых элементов. Я убежден, что посредством чисто математических конструкций мы можем найти те понятия и закономерные связи между ними…». Юджин Вигнер7, физик и математик венгро — еврейского происхождения, лауреат Нобелевской премии по физике в 1963 году, сформулировал фундаментальный философско-методологический закон о непостижимой эффективности математики. Автор книги Клиффорд А. Пиковер8 »Божий ткацкий станок» писал: »Не знаю, математик ли Бог, однако именно математика – тот ткацкий станок, на котором Господь ткет ткань вселенной.… Тот факт, что эту реальность можно описать и достаточно точно вычислить при помощи простых математических выражений, по-моему, означает, что в основе природы заложена математика».
Рис. 1 Адам и Ева
Сальвадор Дали
Таким образом, заручившись поддержкой титанов-учёных из разных стран и эпох, гласящей, что наш мир — это сплошная математика, можно вернуться к событиям, которые происходили с первым человеком на земле — Адамом. Адам9 пребывал в Эдемском саду, где Бог посадил Древо жизни10 и Древо познания добра и зла. Как всем известно, Адам нарушил правило, которое поставил ему Бог. Вкусив плод Древа познания добра и зла, Адам был изгнан из райского сада. Теперь напрашивается вопрос, какое это отношение имеет к предыдущему повествованию? Существует множество толкований понятия мировоззрения еврейскими мудрецами. В данном контексте предложим ещё одну трактовку событий, происходивших в Эдемском саду. Древо жизни и Древо познания определили границу поведения, знаний и возможностей Адама. До изгнания Адама из райского сада у него была возможность »напрямую» без посредников общаться с Творцом. Древо жизни не только давало ему бессмертие, так как понятие Хаим (жизнь на иврите) обозначает соединение с вечностью, но и определяло социальные нормы и ценности поведения человечества — потомков Адама. Древо познания добра и зла: Одна сторона древа — это дерево познания добра — давала возможность раскрываться в своей полноте человечеству, избегая сокрытие, которое существует в этом мире. Эта сторона дерева символизировала гармоничное отношение с Творцом — Адаму было дозволено знать тайны и секреты мироздания. Другая сторона дерева – эта дерево познания только зла, и, нарушив запрет, наложенный Богом, Адам, а впоследствии и всё человечество утратили доступ к секретам и тайнам строения нашей вселенной. (Смотри рис.2 по каббале Даат – ключи знания – не доступны). С момента изгнания наивного Адама и его хитрой жены Евы человечество шаг за шагом раскрывает тайны мироздания во всех его аспектах, стремится к познанию Вселенной, природы и человека.
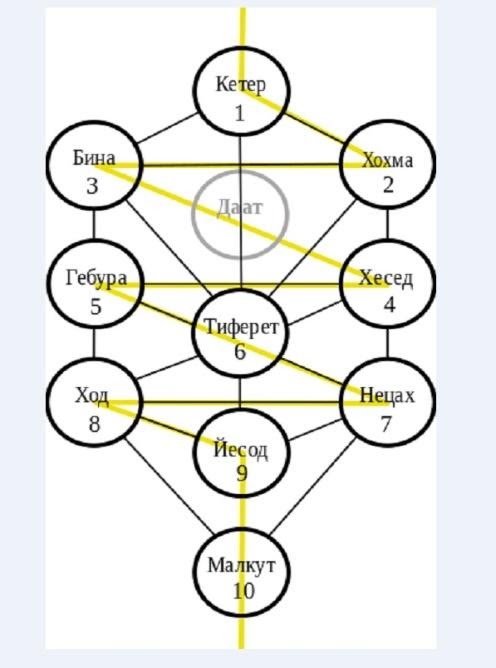
Рис.2
Древо жизни в каббале
Древо Сефирот
Математика изучает разнообразие форм, количественных и качественных отношений в природе и их закономерности. Одной из важных категорий математики является её единство средств и методов.
Создатель использовал таинственное число…?!!!
Боги открыли людям не все. В поиск
пустившись, люди сами открыли немало.
Ксенофан
Бесконечное разнообразие окружающей природы и космической вселенной всегда ошеломляло человечество и являлось движущей силой развития науки и познания. Трудно представить, что 2300 лет назад Греческий философ и математик Евклид11 сформулировал такое уникальное правило: Возможно, разбить прямую линию таким образом, что меньшая часть так относится к большей части, как большая часть относится ко всему целому. В этом случае соотношение между ними всегда даёт иррациональное таинственное число 1.618033.… Прошло всего 1600 лет, и самый известный гениальный математик средневековья Леонардо Пизанский12 по прозвищу Фибоначчи, наверное, заботясь о лучшем питании горожан в родном городе Пиза, рассматривает гипотетическую задачу о разведении кроликов! В результате он приходит к математической последовательности чисел, где каждое число из ряда, придуманного Фибоначчи, разделённое на последующее, даёт уникальное число 1.618 …
Это таинственное число, равное 1,618 является универсальной величиной и нередко его называют числом Бога Леонардо
да Винчи утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной. В природе, искусстве, науке, музыке и архитектуре эта численная величина получила название »Золотое сечение», »Золотое отношение», »Золотая пропорция»13 и »Божественная пропорция»14. Золотое сечение — это и есть универсальное понятие гармонии. Астролог и физик Иоганн Кеплер15 называл золотое сечение одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как универсальное правило, отражающее универсальную и гармоничную структуру нашего мироустройства. Далее шаг за шагом раскроем суть золотого сечения и покажем его важнейшую роль и в геометрии живой природы, и в творениях человека. Золотое сечение закладывают в основу произведений живописи, музыки, скульптуры и архитектуры.
Древние Греки — это современные евреи
Геометрия владеет двумя сокровищами: одно из них — теорема Пифагора, другое — деление отрезка в крайнем и среднем отношении. Первое можно назвать мерой золота, второе же больше напоминает драгоценный камень.
И. Кеплер (1571-1630г.)
Рафаэль Санти. Афинская школа
Древняя Греция оказала огромное воздействие на формирование западной современной культуры и науки.
Целая плеяда таких гениальных математиков как Пифагор, Архимед и Евклид, таких философов как Аристотель, Платон и Демокрит внесли огромный вклад в научный прогресс человечества. Это уникальное явление, в рамках которого активно развивались знаменитая культура и наука, возникло именно в период классический эпохи Древней Греции. Именно в этот период установился новый политический строй – демократия, т.е., власть демоса – всего мужского гражданского населения.
Этот период характеризуется началом законодательной отмены господства богатых землевладельцев и торговцев в управленческих структурах. В каждом городе функционировали театры, работали мастерские, где изготовлялись роскошные произведения искусства: изобразительное искусство, статуи. Зодчие возводили грандиозные постройки. Дети получали общественное образование сначала в школах (греческое »схола – досуг»), где учились известным в то время наукам и искусству, а в подростковом возрасте – в гимнасиях (от »гимнос – раздетый»). Важное место в жизни греческого общества занимала наука16, так как развитие дальней морской торговли, интенсивное градостроительство и освоение новых земель способствовали быстрому развитию математики. Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И, действительно, пропорции пирамиды Хеопса17, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Вместе с этим именно в тринадцати — томном сочинении Евклида под названием «Начала»18, сконцентрированы и подведены итоги знаний, которые создавались и ранее другими античными авторами по геометрии и теоретической арифметике. »Начала» Евклида оставались долгие годы базовым учебником по геометрии. Предшественники Евклида – Фалес, Пифагор, Аристотель и другие много сделали для развития геометрии. Но всё это были отдельные фрагменты, а не единая логическая схема.
Евклид (около 300 до н.э.) работал и писал свои математические труды — »Начала» в Александрии на территории Египта, а не в Афинах, куда Александром Македонским19 был перенесён центр греческой науки, и где переименован один из городов в его честь. По количеству переизданий »Начала» не имеют себе равных среди светских книг. «Начала» публиковались более 2500 раз. Вплоть до XX века книга считалась основным учебником по геометрии не только для школ, но и для университетов. Это была самая первая математическая работа, напечатанная после изобретения печатного станка. Первый выпуск в Европе вышел в 1482 году в Венеции. Книга переведена на множество языков мира.
Будучи школьниками и изучая геометрию (в середине 20- го века), чтобы лучше запомнить, мы применяли поговорку – Пифагоровы штаны на все стороны равны! Евклид почти через 300 лет после Пифагора нарушает нашу школьную идиллию и делит отрезок линии несимметрично, однако, в конце это является самой симметричной пропорцией!
Книга «Начала» Евклида
Думай как математик – простые объяснения
сложной науки
Novavlada.info
Если Вы пугаетесь формул, и математические объяснения в этой главе кажутся сложными, то рекомендую прочитать только то, что выделено в тексте. Для лучшего понимания разобьем текст на четыре логических шага.
Шаг первый – на примере простого отрезка линии выведем понятие золотого сечения20, и его главного и сакрального числа 1.618033… которое будет встречаться на протяжении всей статьи. Определим золотое сечение как гармоничная пропорция.
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, в котором весь отрезок относится к большей части так, как большая часть отрезка относится к меньшей части. Другими словами, меньший отрезок так относится к большему, как больший ко всему.
Рис.3
Золотое сечение обозначается также греческой буквой Ф, φ (число PHI), первой буквой в имени знаменитого греческого скульптора Фидия (490 г. до н. э.), который широко использовал Золотое сечение в своих скульптурах.
Для того, чтобы найти значение φ, введем для длин отрезков AB и AC обозначения:
AB = x, AC = y.
Тогда длина отрезка CB будет выражена формулой:
C = x – y,
причем числа x и y будут удовлетворять неравенствам:
X > 0, y > 0, x – y > 0.
В случае, когда точка C делит отрезок AB в золотом отношении, числа x и y удовлетворяют уравнению:
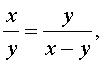
Где
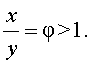
Выведем уравнение для переменной φ:
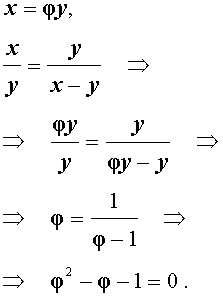
Следовательно,
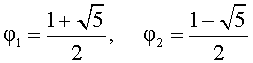
Также необходимо учитывать, что искомое решение уравнения должно быть положительным числом, откуда следует, что ответом получается положительный корень уравнения.
Из этого следует φ > 1 , то второй корень должен быть отброшен.
Итак, золотое отношение
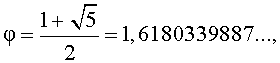
что и требовалось получить.
Величина, обратная этой дроби, отличается от неё ровно на единицу:
Какой бы не была длина отрезков, соотношение между большой составляющей и меньшей составит всегда иррациональное число 1.618…
Шаг второй — это уже переход к плоскостной геометрии и построению сложных фигур с использованием »Принципа Золотой Пропорции».
Пятиугольник, точнее пентаграмма, считался у пифагорейцев священным, поскольку эта фигура симметрична, и в то же время воплощает в себе некоторую асимметрию — золотую пропорцию, полученную соотношением неравных частей отрезка.
Воспроизведем, каким образом: Евклид строит »пентагон» в своём тринадцати томном труде »Начала». Исходным для построения «пентагона»21 является »золотой» равнобедренный треугольник ABD.
Проведем окружность через точки A, B и D (Рис.4). Проведя биссектрису угла ADB до пересечения с этой окружностью в точке Е, мы найдем четвертую вершину Е «пентагона». Заметим, что биссектриса DE проходит через точку С, которая делит отрезок AB в «золотом сечении». Аналогично, проведя биссектрису BF угла ABD до пересечения с окружностью в точке F, мы найдем пятую вершину F «пентагона», после чего можно нарисовать »пентагон» (Рис.3).
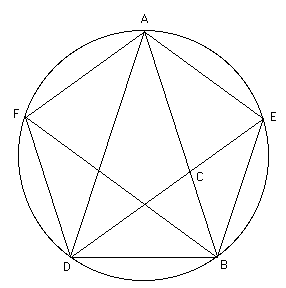
Рис.4 Геометрическое построение пентагона
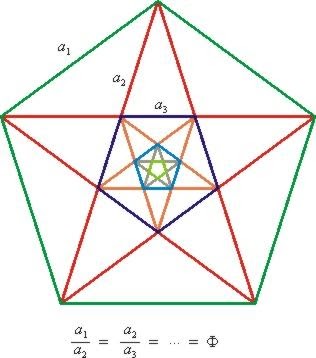
Рис.5. От пентаграммы до золотого сечения
Пентаграмма является звездчатым многоугольником. Правильный пятиугольник – уникальная геометрическая фигура, которую возможно просто построить с помощью линейки и циркуля со значением φ (число золотого сечения):
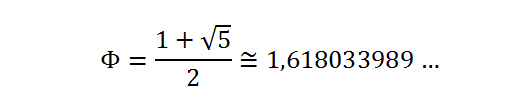
Шаг третий, при котором Евклид переходит от плоскостной геометрии к объёмной, и в 13-ой книге »Начала» описывает объёмную фигуру 12- граника додекаэдра, в основе которого лежит пентаграмма. Додекаэдр является главным из пяти Платоновых тел.
Додекаэдр – магическая фигура
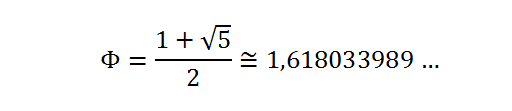
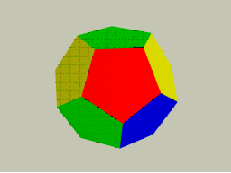
Рис. 6
Используя «пентагон» на Рис.4, Евклид затем строит додекаэдр (Рис.6). Додекаэдр22 в переводе с древнегреческого языка означает двенадцать. Додекаэдр составлен из 12 правильных пятиугольников, которые являются его гранями. Додекаэдр – это »Платонова тело», воплощающее пропорции Золотого Сечения и считающееся с древних времён волшебной, магической формой, гармонизирующей пространство и выражающей принцип творения. Платон утверждал, что именно его »Бог использовал для планирования Вселенной в качестве образца…».
Рис.7
Наиболее известный сферический многогранник — это футбольный мяч, рассматриваемый как сферический усечённый икосаэдр (многогранник с 20 гранями).
Рис. 8 Платон – фреска
Hемного о Платоне. Философское учение Платона дошло до настоящего времени и оказало немалое влияние на современную философию. Платон — древнегреческий философ, ученик Сократа, учитель Аристотеля (между 429 и 427 до н. э. — в Афинах в 347 до н. э.). Сердцевина философии Платона – учение об идеях. Божественное начало, по Платону, немыслимо и непознаваемо. Он придерживался одного из тезисов: »мышление и бытие – это одно и то же». Платон признает доступным пониманию и науке лишь одно — все, что содержалось в замысле вездесущего бога.
Трудно представить сегодня взрослого мужчину или женщину, которые не были бы знакомы ещё с одним важным философским наследием Платона – темой любви. Платон считал, что настоящая любовь бывает только к идее. Поскольку душа – идея, то человек любит в другом человеке именно душу, а тело лишь постольку, поскольку оно просветлено прекрасной разумной душой. Любовь только к телу – неподлинная; она не приносит радости. Ошибка души, ослепленной вожделением, противоположна любви. Любовь – эрос – есть стремление к вечной и прекрасной душе. Поэтому душа устремляется ко всему, в чем видит отражение прекрасного. Это мы называем платонической любовью.
Шаг четвёртый — завершающий. Речь пойдёт о создании математического ряда чисел Леонардо Пизанским в XIII веке, известным под прозвищем Фибоначчи. Ряд чисел который построил Фибоначчи, даёт такое же сакральное число, как и в золотом сечении Греков 1,618 или 0,618. Таким образом, Фибоначчи обобщает понятие золотого сечения и даёт ответы на различные природные процессы, используемые в ряде решений научных задач.
23 ноября в мире отмечается День Фибоначчи — он посвящен первому крупному математику средневековой Европы Леонардо Пизанскому. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Он родился в Пизе (ок.1170 -1250 гг.) в богатой купеческой семье. В молодости Леонардо много путешествовал, сопровождая отца в деловых поездках. Молодой Леонардо посетил по торговым делам Алжир, там он изучал математику у арабских учителей. При поездках в Египет, Сирию, Византию и Сицилию он ещё ближе познакомился с достижениями античных и индийских математиков. Накопив знания по математикe
Леонардо написал ряд математических работ, ставших революционными для средневековой западноевропейской науки. В этих трактатах Леонардо впервые в Европе изложил десятичную систему счисления. Там впервые использовались отрицательные числа, которые обозначали долг. Самым известным его трудом стала «Книга абака» (абак — это древнеримские счёты). Числовой ряд, носящий сегодня его имя, вырос из проблемы с кроликами, которую Фибоначчи23 изложил в своей книге «Liber abacci», написанной в 1202 году.
»Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?»
Можете убедиться, что число пар в каждый из двенадцати последующих месяцев будет соответственно:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
В результате получилось, число пар кроликов создает ряд, каждый член в котором — сумма двух предыдущих.
Например: 3 + 5 = 8; 5 + 8 = 13 и т.д.
Одно из главных особенностей этого »золотого ряда» в том, что отношение каждого последующего его члена к предыдущему неуклонно приближается к показателю 1,618. Математикам он известен как число Фи.
Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Обратите внимание, как значение соотношений колеблется вокруг величины 0,618, причем размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.
Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618 и 1,618.
Отношение любого числа к следующему за ним через одно приближается к 0,382, а предшествующему через одно — 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.
Золотой прямоугольник
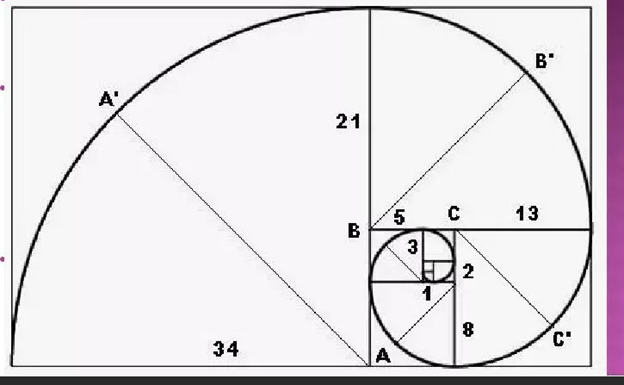
Рис. 9
На рисунке 9 изображён »Золотой прямоугольник»24 со сторонами 34 и 21 (34/21 = 1.6190 = Фи). Последующие прямоугольники так же построены с отношением сторон прямоугольника Евклида рис.2 и с размерами, соответствующими ряду Фибоначчи. Система прямоугольников построена таким образом: отрезая от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, получаем следующий золотой прямоугольник, но меньшего размера. Продолжая отрезать квадраты, мы будем получать всё меньшие и меньшие золотые прямоугольники. Если соединить плавной линией углы полученных на рисунке прямоугольников, получим логарифмическую спираль, полностью повторяющую геометрию завитой раковины. Подобную раковину и соответствующую ей спираль изучал ещё Архимед. В настоящее время закономерность спирали широко применяется в технике.
Длительный »отдых» – да! Случайность – нет!
Чудо не противоречит законам природы,
а лишь нашим о ней представлениям.
Святой Августин
Возвратимся к истории! На Балканском полуострове и ещё на многих островах Эгейского и Средиземного морей располагалась Древняя Греция. Там жили и здравствовали воинственные греки, очень любили спорт, философию и математику! Яркий пример этому Пифагор. Он и его школа внесли огромный вклад в науку, которую в свою очередь Евклид методично и подробно изложил в своём математическом труде — »Начала». По своей сути »Начала» ознаменовали конец периода развития науки и математики, в частности. Многие века не было настоящего прорыва в науке и математике, которую дали нам древние греки. После первых столетий новой веры, все крупные государства Античного мира вошли в эпоху кризисов.
После распада Римской империи наступили «Темные века». Многие империи распались на мелкие княжества и вскоре стали добычей соседних варваров. Затем эпоха распада империй сменилась эпохой переселения народов. В Средневековье богословы не одобряли античную мудрость; об ученых — говорили, что они «ум свой ставят в Бога место». Это всё замедлило развитие науки на многие тысячелетия. Рукописи древнегреческих учёных дошли до наших дней, только благодаря тому, что в монастырях монахи переписывали их дословно, не вникая в смысл того, что написано. Настоящий прорыв в математике через 1600 лет после Евклида в 1202 году произвёл Леонардо Фибоначчи из Пизы в написанной им книге »Абака». Позднее Фибоначчи написал реферат «Практическая геометрия» и «Книгу квадратов». В них впервые были изложены (на латыни) правила действий с нулем и отрицательными числами, а также появились знаменитые числа Фибоначчи.
Сакральное число 1.618…25полученное Леонардом и золотая пропорция пифагорейцев и Евклида является не случайным совпадением, а подтверждает тот факт, что у природы есть какие-то предсказуемые явления.
Если бы Бог создал вселенную полностью со случайными процессами, тогда никакая наука и математика не смогли бы описать происходящее в мире. Мы бы жили в царстве хаоса и катастроф. Сейчас в самый раз вспомнить знаменитый спор двух титанов науки в начале 20-го века, которые принципиально изменили физические законы строения нашего мира. Этот спор межу Альбертом Эйнштейном и Нильс Бором26 занимал их на протяжении нескольких лет, в котором они выясняли »Играет ли Бог в кости»27. Эйнштейн считал, что вселенная лишена случайностей, а Нильс Бор доказывал, что существуют случайные процессы, результат которых можно предсказать только с помощью вероятностных моделей. Апогеем этого научного спора стала конференция 1927 года. Нильс Бор призывал: »Эйнштейн, перестань говорить Богу, что делать», который в свою очередь непоколебимо утверждал, что »Бог не играет в кости». А теперь возвратимся к вселенской драме, которая произошла в райском (Эдемском) саду. Бог наказал Адама, изгнал его из райского сада, отлучил его и всё человечество от секретов мироздания. Образно говоря, с тех пор существует непреодолимая прозрачная »стена» между Богом и людьми. С Его стороны всё построено без всяких случайностей, не хаотично, и всё находится только в закономерной гармонии. Эйнштейн считал, что невозможно понять сущность природы Бога. Мы же пытаемся понять законы вселенной, в которой живём, и поэтому важнейшее место в познавательной деятельности человечества занимают методы научного моделирования, при которых существуют и случайные процессы. Решение данных явлений всегда осуществляется с помощью вероятностно-статистических методов. А Бог-то с другой стороны »стены», он ни в какие кости не играет!!!
Спираль развития науки
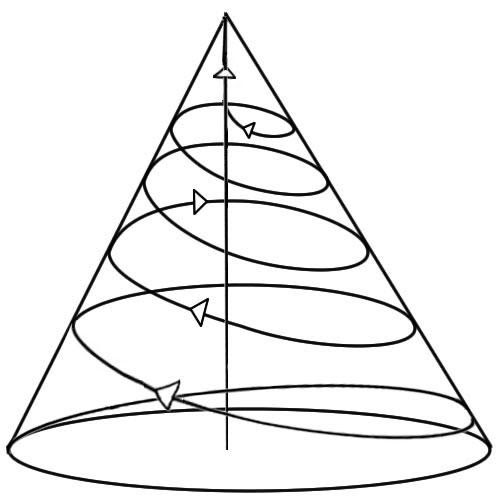
Рис.10
На данном рисунке схематично и наглядно показан процесс развития науки в виде спирального конуса. Ясно видно, что на каждом витке истории показан вектор эволюции, прогресса и накопления научных знаний. Прорыв в науке — открытие качественно нового знания28 означает переход с одного витка на другой. Могу предположить, что вершина конуса недосягаема для науки, так как там и располагается прозрачная недосягаемая »стена».
Яркий пример фундаментальных открытий, которые привели на новый виток знаний, — это гениальные открытия Исаака Ньютона и Альберта Эйнштейна.
Яблоня Ньютона
Согласно общеизвестной легенде, в один из жарких дней 1686 г., Исаак Ньютон отдыхал под яблоней в саду Кембриджского университета. После упавшего ему на голову яблока он сделал важнейшее фундаментальное открытие закона природы. Он сформулировал универсальный закон притяжения, который одинаково притягивает к Земле и яблоко, и Луну. Это — сила взаимного притяжения. На протяжении более 200 лет основными законами физики, определяющими движения материальных тел и их взаимодействие друг с другом, служили три закона Ньютона и его закон всемирного тяготения. Трудно себе представить, что если бы вовремя собрали урожай яблок с деревьев, то научный прогресс мог бы и не произойти!!!
Пришло время другого гения! В начале ХХ века идеи Альберта Эйнштейна произвели полный переворот в науке. Это была настоящая революция в физике, которая полностью изменила понимание человечеством мироустройства и подняла науку на абсолютно новый уровень. Теперь мы знаем, что всё в мире относительно! По теории относительности29 Альберта Эйнштейна при определённых условиях траектория падения »яблока Ньютона» могла бы и не совпасть с головой гениального физика! В 1905 году Эйнштейн, ещё очень скромный служащий третьего разряда патентного ведомства в швейцарском Берне, опубликовывает свою специальную теорию относительности в журнале «Анналы физики». Она была настолько необычна, что на неё вначале никто не обратил внимания, так как она была построена только на гениальных умозаключениях без эмпирического подтверждения и не содержала ни одной ссылки на работы других учёных. А в 1915 году уже знаменитый учёный Эйнштейн представляет свою общую теорию относительности в Прусской академии наук в Берлине. Его идея четырехмерного пространства и времени, которые подвержены деформации, заложила основы современной физики и космологии. Сегодня теория относительности — один из краеугольных камней науки. Она сыграла важную роль в изучении теории Большого взрыва и появления черных дыр во Вселенной, благодаря этому открытию космические корабли сегодня бороздят её просторы, а современный мир получил бесценный подарок — спутниковую систему навигации и т. д. Законы Исаака Ньютона стали частным случаем в общей теории относительности Альберта Эйнштейна.
Сегодня же каждый школьник знает простую на первый взгляд формулу E=mc2, открытую Альбертом Эйнштейном. Теория «большого взрыва» построена на том, что эта эйнштейновская формула действует в обоих направлениях: не только материю можно превратить в энергию, но и энергия может быть превращена в материю. Сам гениальный учёный рассказывал, что послужило толчком написания специальной теории относительности: «Я сидел на своем стуле в патентном ведомстве Берна. И вдруг у меня случилось озарение: если человек парит в невесомости, то он не будет ощущать свой собственный вес. Я был ошарашен»30. Чарли Чаплин говорил Эйнштейну: «Люди Вам аплодируют потому, что Вас не понимает никто, а мне — потому, что меня понимает каждый».
Бог даёт нам намёки
В Библии и в Каббале считается, что в самом имени Бога скрываются тайны мироздания. Речь пойдёт об имени Бога! Код, способ, которым мы можем с Ним общаться! Событие, описанное в 14-й главе библейской книги »Исход»31 повествуется о том, как Моисей раскрыл Красное море и провел израильтян по дну морскому. Чтобы пересечь Красное море, и не утонуть в воде, Моисей стал молиться Богу и просить его о помощи, на что Творец ответил: »Что ты взываешь ко мне?». И тогда Моисей использовал силу 72 Имен Бога и сделал шаг в бездну. И только тогда воды расступились. Это учит нас тому, что путь к результату — это не только направлять просьбы и правильные слова к Богу, молится и уповать на него, но и действовать — мы должны прилагать усилия, как это сделал Моисей, который первым шагнул в ещё не расступившиеся воды. Наряду с 72 именами Бога32, имеется собственное имя Бога33, которое в иудаизме принято не произносить вслух, так как по одной из версий считается, что потеряно его правильное произношение.
Это имя на иврите пишется таким образом:
יהוה
Каждая буква на иврите имеет числовое значение. Получаем числа 10,5,6,5, представим их как натуральное число 10565, и разделим его по пропорциям золотого сечения. Получится 105 и 65. 105 -62% 65-32%, разделив число 105 на 65 то получим 1.61 практически число золотого сечения – число Бога.
Строение участка спирали молекулы ДНК
Рис.11
Золотое сечение является частью нас самих. Рассмотрим, по каким законам выстроена ДНК, в которой спрятана целая информация нашего тела. В 1990 году французский исследователь Жак Перез34, работавший в тот период научным сотрудником фирмы IBM, сделал открытие в области генетического кодирования. Он открыл математический закон, управляющий информационными частицами внутри ДНК. Он обнаружил, что эти частицы, органические соединения (нуклеотиды) в ДНК, организованы в структуры дальнего порядка, называемые резонансами. Резонанс представляет собой особую пропорцию, обеспечивающую разделение ДНК в соответствии с числами Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …). Цепь ДНК35 напоминает плотно скрученную двухстороннюю спираль. Этот код, на котором запрограммирована вся наша жизнь, начиная от внешнего строения тела, цвета глаз, волос и заканчивая характером, вкусом, предпочтениями. ДНК является универсальным био-математическим законом, который указывает на высочайший уровень самоорганизации клеток. Две спирали ДНК скреплены между собой мостами. Именно эти мосты находятся через каждые 10, 5 , 6, 5 аминокислот которые даёт жизнь клетке ДНК — дают нам жизнь.
Получается, что в каждой клетке ДНК Бог расписался своим именем יהוה.
Исторически сложилось, что множество научных открытий, эволюционных процессов и решение различных проблем происходит от общего к частному, от макро к микро. Это и есть дедуктивный метод. Так и в данном случае изучение анатомии человека, форм, психологии человека занимало учёных много столетий до открытия ДНК — его первостепенной роли в хранении генетической информации. Полное открытие и описание ДНК, пришлось только на пятидесятые годы прошлого столетия.
Живопись — это поэзия, которую видят, а поэзия — это живопись, которую слышат.
Леонардо да Винчи
Известно, что изучение человеческого тела и его пропорций началось за много столетий до начала итальянского ренессанса. Повторное открытие математических пропорций человеческого тела, сделанное Леонардо да Винчи в XV веке, стало одним из великих достижений, итальянского ренессанса. Рисунок кисти Леонардо да Винчи примерно в 1490-92 годах являлся иллюстрацией для книги, посвященной трудам Витрувия36. На нем изображена фигура обнаженного мужчины в двух наложенных одна на другую позициях: с разведенными в стороны руками, описывающими круг и квадрат. Термин «Золотое сечение» ввел Леонардо да Винчи. Он считал, что человеческая фигура — самое совершенное творение вселенной.
«Витрувианский человек» – изображение
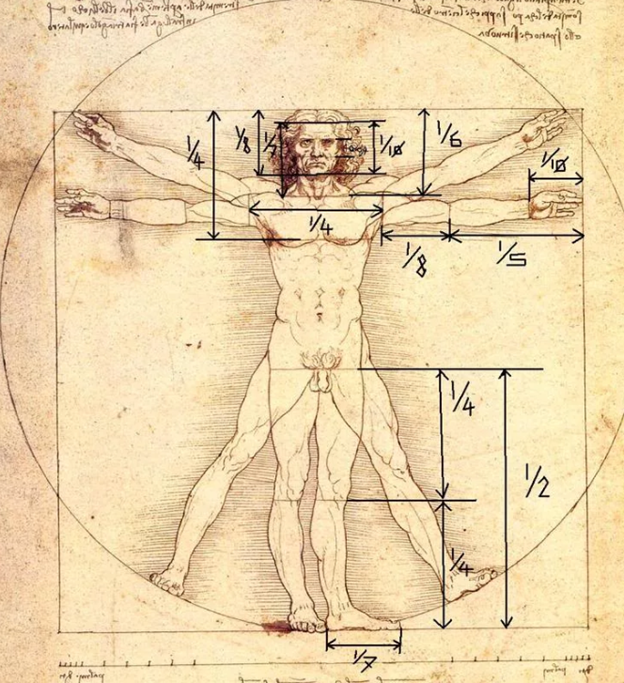
Рис. 12
В сопроводительных записках Леонардо да Винчи так описал соотношения, являющиеся «божественной пропорцией»:
Расстояние от кончиков пальцев до запястья равно 1:1,618;
Расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618;
Расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618;
Расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 и др.
Знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал золотое сечение в своих произведениях. Золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.
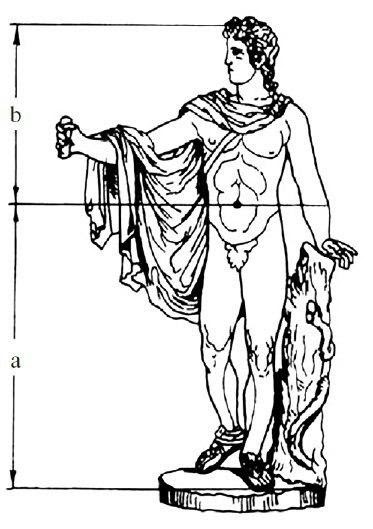Рис. 13
Самая загадочная улыбка в мире!
У многих имя Леонардо да Винчи ассоциируется с портретом «Мона Лиза»38. Более пяти столетий учёные и искусствоведы пытаются разгадать, что кроится за еле заметной улыбкой женщины на полотне «Мона Лиза». Эта картина является самым популярным экспонатом Лувра, — вообще, самое известное произведение изобразительного искусства в мире. Сопоставим несколько известных фактов:
Мона Лиза (Джоконда) не была написана художником на продажу (бытует мнение, что это был заказ торговца шелком Франческо дель Джокондо), так как Леонардо оставил полотно в своей мастерской. Да Винчи не расставался с ней почти до конца жизни. Лишь незадолго до смерти гения его ученик Франческо Мельци, которому «Мона Лиза» досталась от Леонардо в наследство, продал полотно королю Франции.
Мона Лиза – безусловно, женский портрет, но моделью являлся молодой женоподобный юноша! Существует удивительное сходство практически полная идентичность лиц на картине «Иоанна Крестителя»39 и Мона Лизы. Точно известно, что моделью «Иоанна Крестителя» являлся юноша, его любимый ученик Джан Джакомо Капротти, по прозвищу Салаи — от итальянского «дьяволенок». Их длительная связь продлилась более четверти века — как предполагается, и их интимные отношения. Да Винчи дорожил этим полотном – на протяжении многих лет любовался своим детищем, время от времени поправлял и дорисовывал. При написании да Винчи применял особую технику, основанную на принципе рассеивания линий, отсутствие четких границ между предметами. Именно благодаря ей улыбка Моны Лизы приобрела свое удивительное мерцание. Важный факт — да Винчи написал портрет, используя пропорцию золотого сечения см. рисунок 9 и 14,15
Мона Лиза Рис. 14
Рис.15 Мона Лиза
Самое время подвести итог: »Мона Лиза» написана не на заказ, а для любимого ученика, с которым он не расставался более четверти века. На картине изображена женщина, но позировал молодой мужчина. Видимо художник был полон любви к своему ученику и восхищался его красотой, он послужил моделью его нескольких важных произведений. Особая техника написания »сфумато» (рассеивающая) гениального мастера и соблюдение пропорций золотого сечения — является триумфом мирового искусства, и до сих пор будоражит воображение миллионов людей.
Что общего между Платоном, Леонардо да Винчи, Сальвадором Дали и праздником Пейсах (Пасхой)?
Тайная вечеря, Леонардо да Винчи
Тайная вечеря, Сальвадор Дали, 1955
Рис. 16,17
Леонардо да Винчи и Сальвадор Дали объединяет общая тема двух произведений, связанных с жизненными событиями Иисуса на земле под названием — »Тайная вечеря»40. Платон же с его так называемыми »Платоновыми телами», воплощающими пропорции Золотого, Божественного сечения, нашли место в картине Тайная вечеря кисти Сальвадора Дали41.
Леонардо да Винчи начал писать Тайную вечерю в 1495 году и завершил работу около 1498 года. На фреске гениального художника да Винчи изображена пасхальная традиционная иудейская трапеза (Седер Песах). Тайная вечеря происходила в Иерусалиме на горе Сион на втором этаже над гробницей царя Давида. Центральная фигура Тайной вечери — это сам Иисус Христос. Иисус (еврейское имя Иешуа, что переводится с иврита как »Спасение Бога») — галилейский еврей, говорящий на двух языках – арамейском и древнем иврите. Деятельность Иисуса пришлась на период острого антагонизма между различными религиозными течениями и различными мистическими сектами. Христос, по-гречески »помазанник» – мессия – »машиях» являлся, безусловно, религиозным реформатором, проповедником с фарисейскими взглядами, находившимся под влиянием идей ессейского мистицизма. Христос и его ученики придерживаются иудейских традиций, на стол поданы только пресники. В Евангелии от Матфея читаем: В первый же день опресночный приступили ученики к Иисусу и сказали Ему: где велишь нам приготовить Тебе пасху? Двенадцать апостолов-учеников Иисуса олицетворяют по числу двенадцать колен Израиля. По иудейской традиции самый младший из присутствующих задаёт вопросы главе трапезы, им являлся апостол Иоанн Богослов. Он и обращался с традиционным вопросом к Иисусу: »Что значит все это?». Ещё по обряду проведения праздника Песах говорится о четырёх сыновьях, один из них Нечестивый — его олицетворяет Иуда, продавший своего учителя за небольшую плату. Тайная вечеря — празднование первого дня Песах — была тайной для врагов Христа. Иуда уже заранее вошел в сговор с первосвященниками, так как они искали удобный момент, чтобы схватить и казнить Христа.
Само произведение Леонардо да Винчи выполнил в соответствии с пропорциями золотого сечения. Фреска как будто разбита по горизонтали двумя воображаемыми линиями, которыми художник разделил свое произведение на три равные части (1/3 каждая часть композиции). Если провести диагональ между углами, тогда получится, что фигура Иисуса находится строго посредине, а диагональ пересекает в районе его глаз.
Полотно »Тайная вечеря» Сальвадора Дали была написана в 1955 году. Это полотно является абсолютно мистической работой. Практически трудно понять, что на полотне изображена »Тайная вечеря» – лишь название подсказывает, что это — трактовка классической библейской темы художником. Картина абсолютно симметрична, и Христос делит её на две равные части. Фигура Иисуса почти прозрачна, ещё немного, и она сольётся с безжизненным пейзажем и исчезнет, в то же время угрожающий жест поднятой руки приводит к полному повиновению и безоговорочному послушанию всех двенадцати апостолов. Художник представляет образ Иисуса не милосердным и не обладающим совершенной любовью, а строгим учителем-наставником, который уже готов вознестись к ждущему его Богу-отцу. Бог — отец, изображен выше, с распростертыми руками, обнимающими небо и землю. Христос и двенадцать апостолов помещены в пространство правильного додекаэдра (смотри рис.5) Додекаэдр имеет 12 граней, по количеству апостолов, каждая грань додекаэдра соответствует одному из апостолов. Фигура додекаэдра символизирует Божественное сечение – канонизация святого духа. Великий художник двадцатого столетия прибегнул к символике неба и сотворения всего мира с помощью одного из пяти Платоновых тел, построенных по законам »Божественного сечения».
Кремлёвские звёзды над нами горят…
Рис.18 Звёзды Кремля
Пятиконечная звезда — один из древнейших символов человечества. Её изображение найдено в наскальных рисунках Ближнего Востока, Греции, Японии и Америки. В некоторых культурах пятиконечная звезда символизирует военную доблесть, защиту от опасности. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Пятиконечная звезда построена по законам золотого сечения (см. рисунок 4). В пятиконечной звезде каждая из пяти линий делит другую линию в точке золотого сечения, а концы звезды являются золотыми треугольниками. Золотой треугольник (равнобедренный), потому что отношение длины боковой стороны к длине основания равняется 1,618.
Загадка скрипок Антонио Страдивари
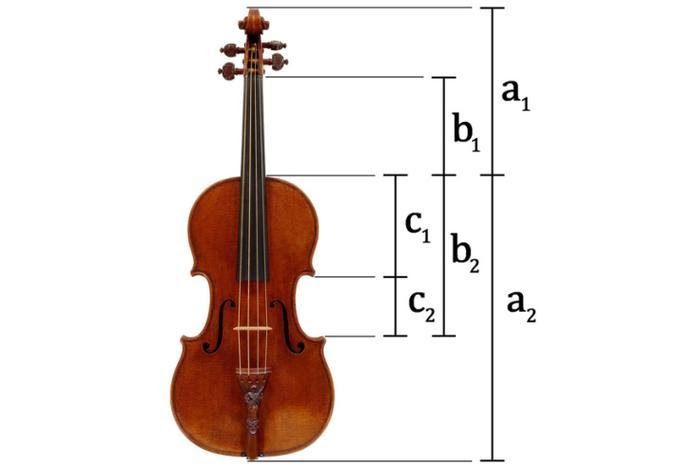
Трудно предположить, что кто — то не слышал о волшебном изготовителе скрипок Антонио Страдивари42, который жил (1644–1737) в городе Кремона, Италия. На чертежах мастера видно, что Страдивари особенно тщательно рассчитывал геометрическое положение прорезей на передней части корпуса, – и помещал их в точки, определенные золотым сечением. Благодаря закону золотого сечения, скрипки Страдивари обладают непревзойденным качеством и звучанием. Скрипка Страдивари, изготовленная в 1721 году, была продана с аукциона в 2011г. за 9,8 миллиона фунтов стерлингов (15,9 миллиона долларов США).
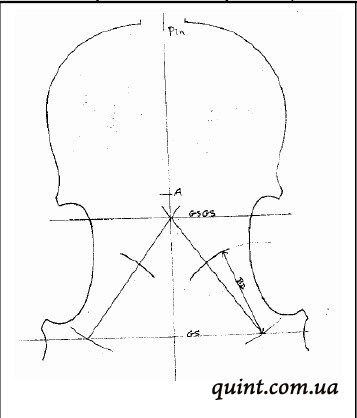
Рис.19
Чертежи мастера Страдивари
Так же важно подчеркнуть, что »секретом» Страдивари называют лак, клей, древесину и, конечно, мастерство изготовителя. Скрипки итальянского мастера и поныне не превзойдены по звучанию и по качеству изготовления.
Золотое сечение на службе дизайнеров
Рис.20
Яйцо как символ зарождения44 – символ Золотого сечения
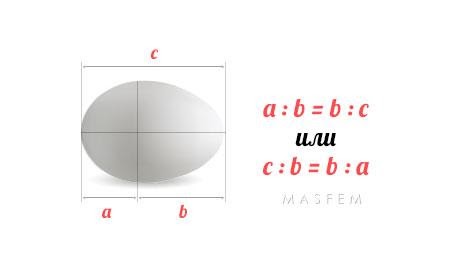
Рис.21
На рисунке видны золотые пропорции яйца птицы.
Яйцо птицы является живой конструкцией идеальной формы с высокой прочностью оболочки по его длиной стороне — c.
А природа с нами не лукавит
Золотая пропорция в природе характеризуется соразмерностью и гармоничностью её строения. Различные природные системы в своём развитии приобретают также функциональную устойчивость во многих случаях по закону золотой пропорции. Существует множество примеров, когда природные явления и процессы развиваются именно по спирали45: по спирали метель закручивает снежные массы. По спирали зарождается и раскручивается ураган, спиралеобразно паук плетёт свою паутину, спираль прослеживается в расположении семян подсолнечника. Более того, спиральную форму имеют некоторые галактики, которые можно разглядеть с Земли.
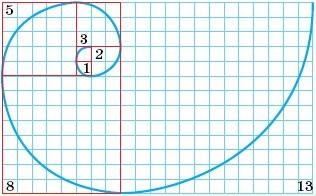
Рис. 22 Спираль Архимеда
(ряд Фибоначчи)
Раковина моллюсков
Рис.23
Установлено что винтовое листорасположение на ветке и расстояние между листьями, составляет дробь (число оборотов на стебле/число листьев в цикле, например 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи. Хорошо известна золотая пропорция пяти лепестковых цветков яблони, груши и многих других растений
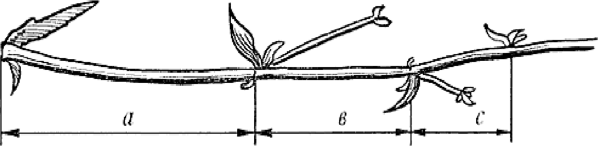
Рис.24
Золотое сечение в живой природе
Рис. 25
Примеры золотого сечения в природе
Уникальность числа 1.618… стоящего у истока золотого сечения объясняется тем, что его использование привносит в науку, музыку, архитектуру и даже природу иногда невидимый, но подсознательно уловимый порядок.
Заключение (для тех, кто дошёл до конца…) — Гармония in
Гармония является началом всей природы. Понятие гармонии в природе ввёл ещё гениальный греческий философ Платон с помощью правильных геометрических тел, называемых »Платоновыми телами». Мы уже упоминали выше одно из Платоновых тел — это додекаэдр – правильный 12-гранник, гранями которого являются правильные пятиугольники, основанные на Золотом Сечении. Проведём несколько подсчётов: число углов на поверхности додекаэдра равно 5×12=60 (что соответствует 60-летнему циклу). Додекаэдр имеет 30 ребер и 12 граней (12 колен израеливых), а произведение этих чисел — 30×12=360. Следуя магической числовой символике додекаэдра, которая отражала числовую гармонию, древние учёные пришли к мысли разбить год на 12 месяцев (число граней додекаэдра), каждый из которых содержал ровно 30 дней (число ребер додекаэдра). Получили календарь, созданный в четвертом тысячелетии до н.э. В этом календаре год состоял из 365 дней. Он делился на 12 месяцев по 30 дней каждый, в конце года добавлялось пять праздничных дней, которые, однако, не входили в состав месяцев. Заметим, что в своей системе измерения времени и угловых величин в древнем мире также использовали »магические» числа додекаэдра.
Всё, что мы обсуждали в данной статье, связано с сакральным иррациональным числом 1.618…. Существуют и другие важные математические величины, например число Пи — . Но это не здесь и не сейчас… впрочем, это уже совсем другая »история»….
Ришон ле — Цион
13 апреля 2021 года
Библиография
1.Сотворение мира | Энциклопедия иудаизма онлайн …
https://toldot.ru › sotvorenie Mira
2.Готфрид Вильгельм Лейбниц цитаты (57 цитат)
Gotfrid- vilgelm – leibnits ru.citaty.net
3.Пифагор краткая биография
obrazovara.ru
4. Платон
Document/ newhilens/ iphlib.ru
5. Альберт Эйнштейн.
Наука и религия = Science and religion
// Nature. — 1940. — Т. 146. — С. 605—607.
Инфельд Л.6. Мои воспоминания Эйнштейн и современная физика:
Сборник памяти Альберта Эйнштейна. — М.: Гостехиздат, 1956. — c. 188.
7. Вигнер, Юджин Пол — статья из энциклопедии «Кругосвет».
8. По материалам сайта Клиффорда Пиковера.
9. Мидраш Берешит Раба, 17:4; Мидраш Бамидбар Раба, 19:3; Мидраш Кохелет Раба, 7:1.
10. Сайт — Познай себя. ДРЕВО ЖИЗНИ — МАТРИЦА МИРОЗДАНИЯ В КАББАЛЕ.
11. Зубов А. Ю. Евклид // Большая российская энциклопедия. Т.9. М., 2007, с.510.
12. Frances Carney Gies Leonardo Pisano//Энциклопедия Британника.
13. Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number.
14. Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
15. Белый Ю. А. Вклад Кеплера в развитие математики и его астрономические исследования // Историко-астрономические исследования. Вып. XI. 1972. С. 65—106.
16. Словарь древнегреческой культуры- Arzamac
Materials / arzamac academy.
17.ОПРЕДЕЛЕНИЕ ХАРАКТЕРНЫХ РАЗМЕРОВ ПИРАМИДЫ ХЕОПСА
ЧЕРЕЗ ЗОЛОТОЕ СЕЧЕНИЕ
С.І. Якушко, к.т.н., доц. СумДУ
18. Рыбников К. Русские издания «Начал» Евклида.
Успехи математических наук, 1941, № 9, стр. 318—321.
19. Бойназаров Ф. Проблемы традиции и современности: (Образ и личность Александра Македонского). — М.: Наука, 1990. — 272 с.
20 Решение геометрических задач методом »Золотого… archive/ https/moluch.ru
21. Mario Livio. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. — Broadway Books, 2002. — ISBN 0-7679-0815-5. 22. Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Эфрона : в 86 т. (82 т. и 4 доп.). — СПб, 1890—1907. 23. Числа Фибоначчи – Джемс Трефил, энциклопедия… Chisla Fibonachi / https // element.ru. 24. Edward B. Burger, Michael P. Starbird. The Heart of Mathematics: An Invitation to Effective Thinking. — Springer, 2005. — ISBN 9781931914413. 25. Божественная пропорция — Google Sites bozestvennoecislo https // Google. Com 26. Ранние годы Нильса Бора Архивная копия от 15 апреля 2009 на Wayback Machine — история, копия. 27. Играет ли Бог в кости: от ядерной физики до… igraet- li- bog…reviews / https // gorky. Media. 28. Планирование и организация производства. Books // https : // books.google.co.il 29. Русский перевод в сборнике: / Под ред. Е. Куранского. — М.: Мир, 1979. — 592 с. — С. 146—196. 30.Эйнштейн, не учите бога, что ему делать: история… Forschung / https: // Germania – online. Diplo.de. 31. Финкельштейн, Израиль. «Раскопанная Библия», 2001. 32 72 имени Бога. История, Значение, Технологии… 8 – znachenie … / content / benoom. com. 33. Йегуда Ашлаг (Бааль Сулам), «Введение в комментарий „Сулам“. Десять сфирот».
34. Симметрия в ДНК и белках — Математические методы…
Simmetriy belkah / https: // stadref.com
35. Bustamante C., Bryant Z., Smith S. B. Ten years of tension: single-molecule DNA mechanics (англ.) // Nature. — 2003. — Vol. 421, no. 6921. — P. 423—427.
36. Витрувиа́нский человек – Livelib
1001077680 / book / https:// www.livelib.ru.
37. Виппер Б. Р. Искусство Древней Греции. — М.: Наука, 1972.
38.Мона Лиза улыбка, описание картины — Лувр
Мона – Лиза // https: mylouvre.su
39.Иоанн Креститель Леонардо да Винчи
Post231907549 // https:// liveinterner.ru
40. » Тайная вечеря» Леонардо да Винчи
Last- sapp… / https:// www. Barcelona – excurs.org
41. Описание картины Сальвадора Дали » Тайная вечеря»
https://opisanie-kartin.com
42. Сергеев Е.Г. Антонио Страдивари / Евгений Сергеев.- Издательские решения, 2020.- 120 с.
43.Золотое сечение – core
https:// core.ac.uk
44.Почему яйцо является символом Золотого сечения…
http:// wiki.tgl.net.ru
45. Щекалева М. А. — Бионическая практика Учебно-методическое пособие.
Иллюстрация: ppt-online.org
